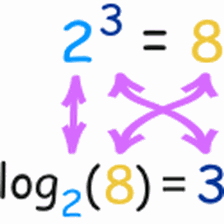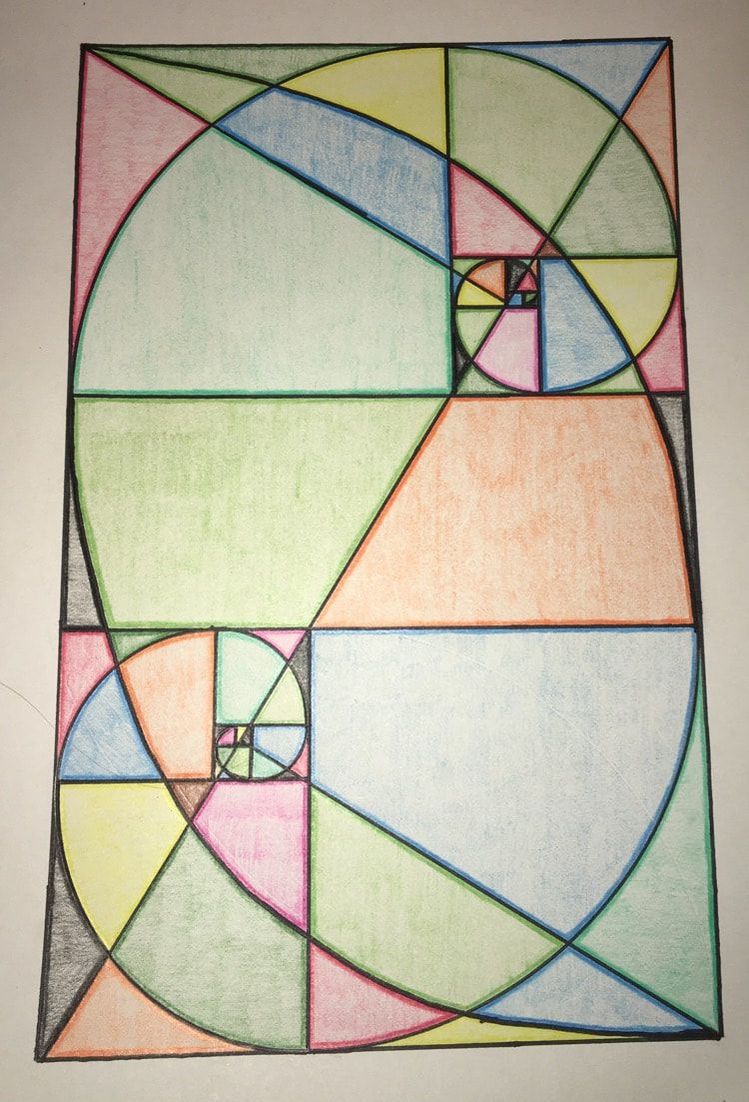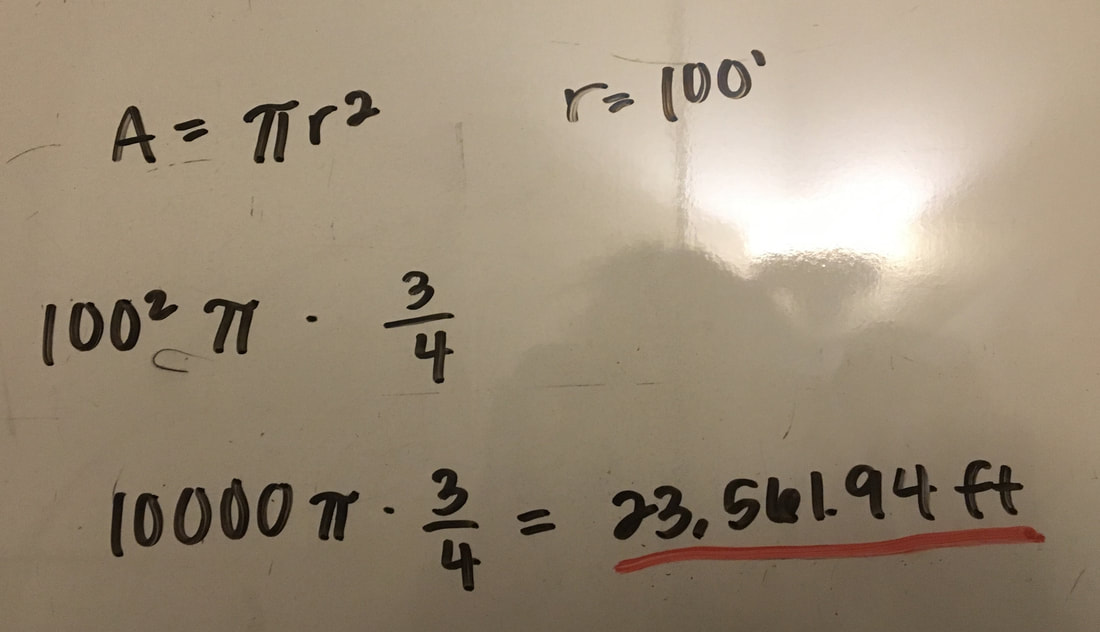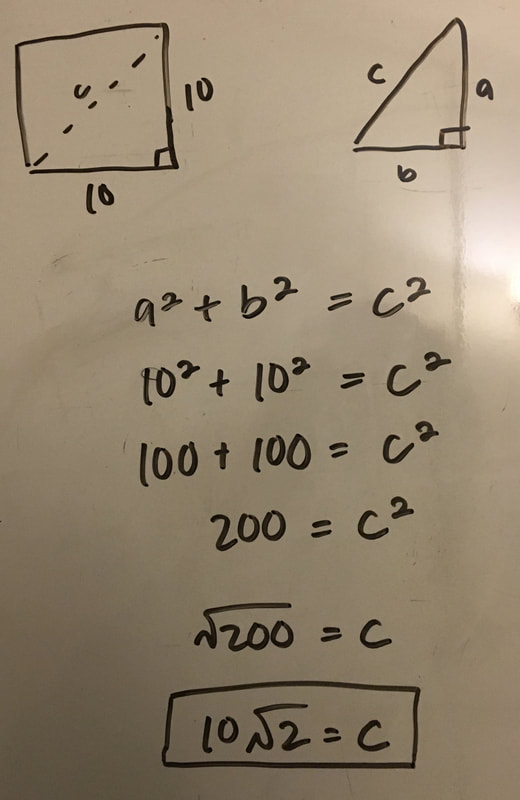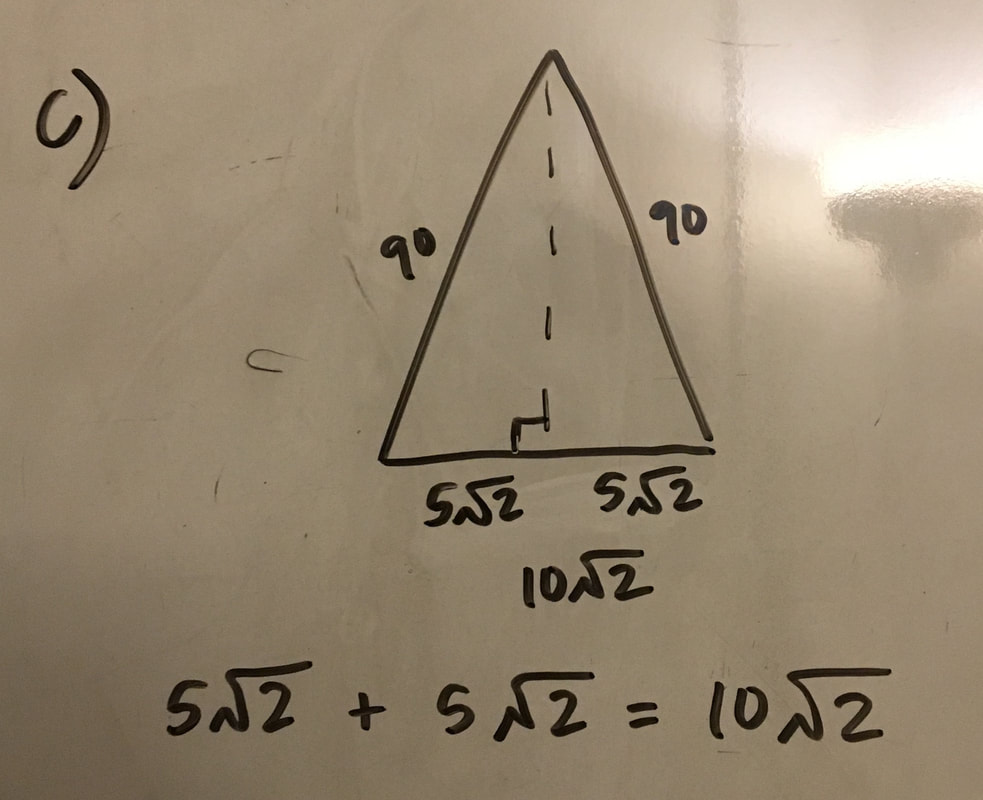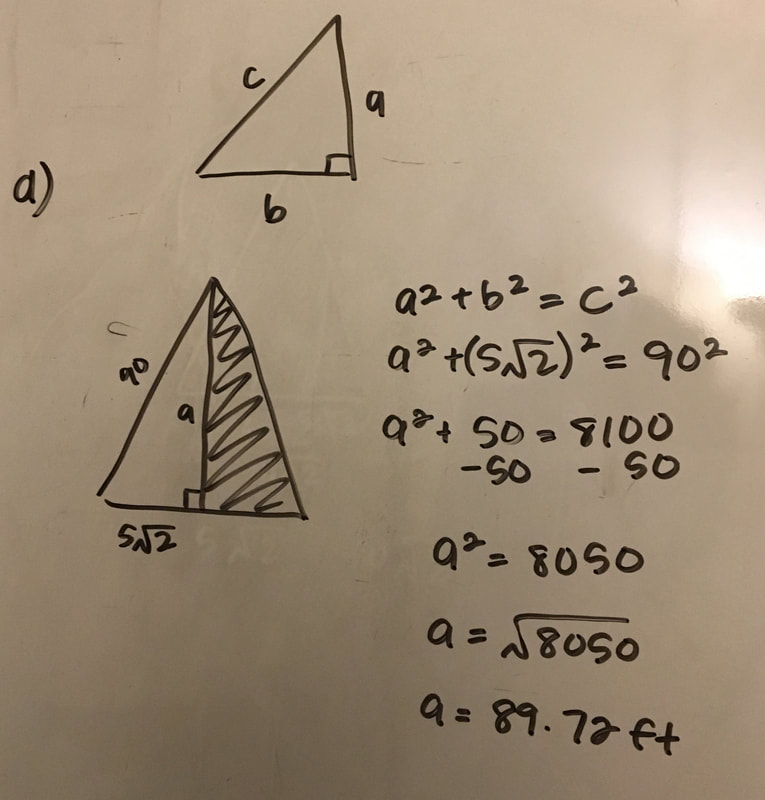End of the Year Math Write Up
Growth Mindset Project
|
For my growth mindset project, I decided to learn how to use Hawaiian poi balls over the two week period. I chose to learn how to use the Hawaiian poi balls because it was something that was sitting in my room for year and years and I never bothered to pick them up and learn. I'm also a part of a Hawaiian outrigger canoe club so I felt that learning how to use the poi balls would immerse myself more into the culture.
The growth mindset project impacted me because it showed me that if you actually put in the time and continuously do something even if you keep failing, eventually you'll learn what you're doing wrong and fix it. I hit myself or hit the poi balls together countless amount of times before I was able to do a run where everything went smoothly. But I eventually was able to get it right because I kept on going and set aside time to keep practicing. I didn't continue to try and improve on my topic after the two weeks over because my priorities were not that anymore. If I was in a dance where I needed to use them, then I probably would have kept it up but nothing was requiring me to continue to learn how to use them. |
This year I found the growth mindset project especially applicable to studying for and taking the SAT. While studying, without growth mindset, I would have never tried to memorize formulas or keep on trying problems on Khan Academy in order to be able to answer more problems correctly on the SAT. Also taking the SAT can be very intimidating. Growth mindset helped me work through the more challenging problems during the test, and sometimes being able to persevere got me to an answer!
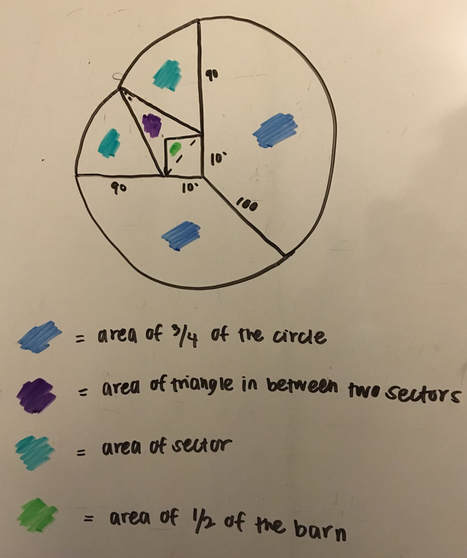
The Cow ProblemProblem Statement: There is a 10' by 10' barn. A cow is attached to a corner of the barn with a 100' rope. We need to figure out what area of land the cow can graze. We used our learning of finding areas of different shapes to solve this problem.
I really enjoyed solving this problem because it was like breaking down a puzzle to figure out how the whole thing works. I liked how it pushed my thinking. I asked myself a lot through the unit, "What is the shape telling me? What am I missing?" It challenged me to think outside of the box and broadened the way I look at problems. |
Logarithms
|
Logarithms are an extension of exponents. In order to understand logarithms, you need to know the principle rules of adding, subtracting, multiplying, and dividing exponents. In this unit we learned how to manipulate exponents and turn them into logarithms as well as turn logarithms back into exponents. We also learned how to expand more complex exponents into logarithmic form.
I really enjoyed learning about logarithms because it challenged me. It was hard to adjust to the format of them and how you read one out. I feel like expanding the exponent gave me a better understanding of the exponent and all of its aspects, which in turn made me more fluent in exponents. |
This year I have grown in the way I interact with adults and older mentors. Internship forced me to become more of a "people person." I could no longer rely on my mom or a teacher to introduce me or talk about my achievements. I had to be the one to do these things on my own. Internship taught me how to hold a conversation, how to present myself, and how to be friendly. It gave me more confidence to walk into the real world and tell people who I am and what I am about. Below are some people, in action, that I was able to talk to during my internship, using my new "people person" skills:
Next year, I am taking calculus because I want to be a civil engineer and engineers need to know calculus to do their job correctly. I know I am going to need to take calculus in college as well, so taking it my senior year would give me a good understanding of it before taking the college version of it. I also feel confident with algebra and up for the challenge of calculus.
Next year, I plan on continuing study groups to be successful in math. Study groups really worked for me for studying for the SAT, it made me accountable and set aside a time specifically for studying. I talked with some people who are taking calculus next year and we already agreed to be a study group and support system next year.
Next year, I plan on continuing study groups to be successful in math. Study groups really worked for me for studying for the SAT, it made me accountable and set aside a time specifically for studying. I talked with some people who are taking calculus next year and we already agreed to be a study group and support system next year.
Honors
|
Honors this year was a positive experience. I think, especially towards the beginning of the year, I enjoyed receiving packets that pushed my thinking of the original packet. Trying to figure out the elevated concept on my own helped me understand the core concept even better.
During the honors project this year I learned that I can be a very efficient worker. I learned how to multi-task. That was a very busy time, with three different projects I needed to work on to be exhibited at Festival del Sol. I found myself memorizing lines for our sketches while working on the drawing of my Fibonacci spiral. I learned that I am good at utilizing my time wisely. To the left is my drawing showcasing the Fibonacci Sequence. Something I suggest to improve honors next year is to provide more additional topics to learn. Sometimes I feel like the honors problems were just the same as the originals but with more numbers. I would like to see more learning of more complex units, maybe more pre-calculus to prepare for senior year. |
Around King Arthur's Table Write Up
Problem Statement
Every time he had a prize, King Arthur would play a game with his knights to see who would be the lucky winner. The knights would sit at King Arthur's round table and wait for him to stand behind their chair. King Arthur would always start at chair 1 and say, “You're in.” Then, he would stand behind chair 2 and say, “You're out.” Next, he would stand behind chair 3 and say “You're in.” When King Arthur would circle back to chair 1 he either said “You're in” or “You're out”, depending on what he said to the previous knight. If there was an empty chair, he would skip it. He did this around the table until there was only one knight in. That knight was the winner.
The number of knights was different each time. The big question is if you knew how many knights were going to be at the table, how could you quickly determine which chair to sit in so that you could win? We had to develop a general rule, formula, or procedure that would predict the winning seat in terms of the number of knights present.
The number of knights was different each time. The big question is if you knew how many knights were going to be at the table, how could you quickly determine which chair to sit in so that you could win? We had to develop a general rule, formula, or procedure that would predict the winning seat in terms of the number of knights present.
Process
|
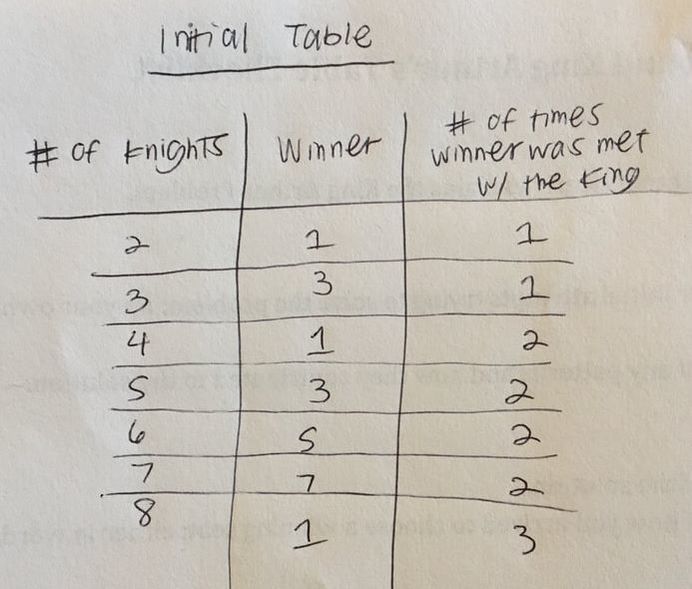
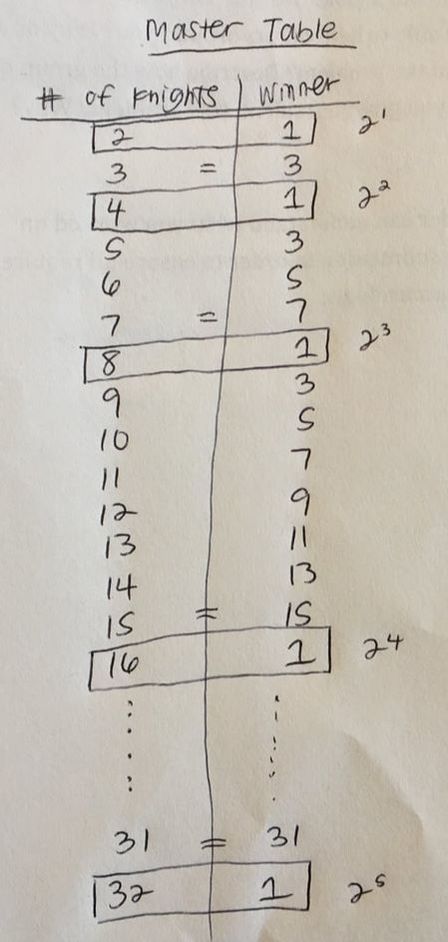
My initial attempt at solving this problem was to create a table that consisted of the number of knights, the winning seat, and the number of times the winner was met with King Arthur. When my group shared our different approaches, I found that keeping data on the number of times the winner was met with King Arthur was not going to be useful in the problem. From this knowledge, we were able to condense our different tables together to create a master table of the number of knights to the winning seats. |
|
From this master table, we found many patterns.
These patterns contribute to our solution because you know that the winner can never be an even number and the pattern is growing exponentially. However, it stops growing exponentially and resets to the number one after every base two exponent. These are aspects that you have to incorporate or think about in your final solution. |
Solution
Our final solution ended up being that you take the number of knights and subtract it by the nearest greatest integer of a base two exponent. With that difference you multiplied it by two and added one to get the winning seat.
We arrived to this solution just by identifying patterns in our master table. We created an initial formula and tried it out with a value from our table. If the formula didn't work we would tweak it based on what didn't work previously. The only way we were 100% sure if a formula worked was if it worked for three values in our table.
The final formula we came up with was w = 2(k - 2^?) + 1. W is the winning seat and k is the number of knights. 2^? is the nearest greatest integer of a base two exponent.
We arrived to this solution just by identifying patterns in our master table. We created an initial formula and tried it out with a value from our table. If the formula didn't work we would tweak it based on what didn't work previously. The only way we were 100% sure if a formula worked was if it worked for three values in our table.
The final formula we came up with was w = 2(k - 2^?) + 1. W is the winning seat and k is the number of knights. 2^? is the nearest greatest integer of a base two exponent.
Evaluation / Reflection
The thing that pushed my thinking was the logarithms. This problem required us to utilize the skills that we learned previously, which were a bit rusty. Trying to find a formula with a logarithm in it was probably the trickiest thing when it came to this problem. I was challenged with this aspect because I had never incorporated logarithms before into an equation and I didn't know about the greatest integer function.
I feel like I can recognize when I need help with a task. When I am stuck and have no idea where to go, that's when I know I should look for someone to guide me somewhere. I think I am confident to ask for help when I need it because sometimes I'm not sure if what I'm doing is right or useful and it's good to get another set of eyes on my work. I think I am able to help others around me because during this problem Teagann asked me a lot of questions and I think I was able to help her understand the problem a little better.
My group interacted very well during the beginning stages of this problem. We each shared what we did and then we were able to combine our tables together because we communicated. The group quiz affected my learning in a positive way because my group was able to find a formula for the new problem using the skills and tools we learned from the original problem. We also had Mr. Carter teach us something new during the test with a logarithm rule and greatest integer function. I would give myself an A on this problem because I actively participated and communicated with my peers and asked questions to better understand the problem.
I feel like I can recognize when I need help with a task. When I am stuck and have no idea where to go, that's when I know I should look for someone to guide me somewhere. I think I am confident to ask for help when I need it because sometimes I'm not sure if what I'm doing is right or useful and it's good to get another set of eyes on my work. I think I am able to help others around me because during this problem Teagann asked me a lot of questions and I think I was able to help her understand the problem a little better.
My group interacted very well during the beginning stages of this problem. We each shared what we did and then we were able to combine our tables together because we communicated. The group quiz affected my learning in a positive way because my group was able to find a formula for the new problem using the skills and tools we learned from the original problem. We also had Mr. Carter teach us something new during the test with a logarithm rule and greatest integer function. I would give myself an A on this problem because I actively participated and communicated with my peers and asked questions to better understand the problem.
Maximum Rectangle Write Up
Problem Statement
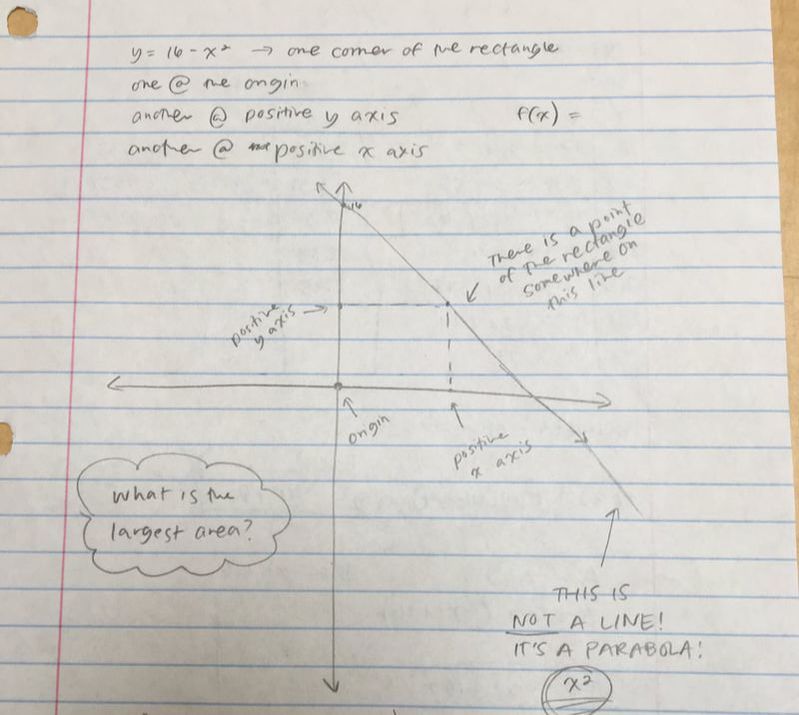
A rectangle has one corner on the graph of y = 16 - x^2 , another at the origin, a third on the positive y-axis, and the fourth on the positive x-axis. If the area of the rectangle is a function of x, what value of x yields the largest area for the rectangle.
Process
|
My initial attempt at this problem was to draw out a graph with all four quadrants (shown to the right). I plotted a point at the origin and graphed y = 16 - x^2. Once I drew the line, I chose a random spot on the line and plotted a point there. My last two points met up the point on the line to the positive x and y axis. However, after discussing as a class, I realized I made the mistake of drawing a line instead of a parabola. If something is squared in a function that means it is a parabola.
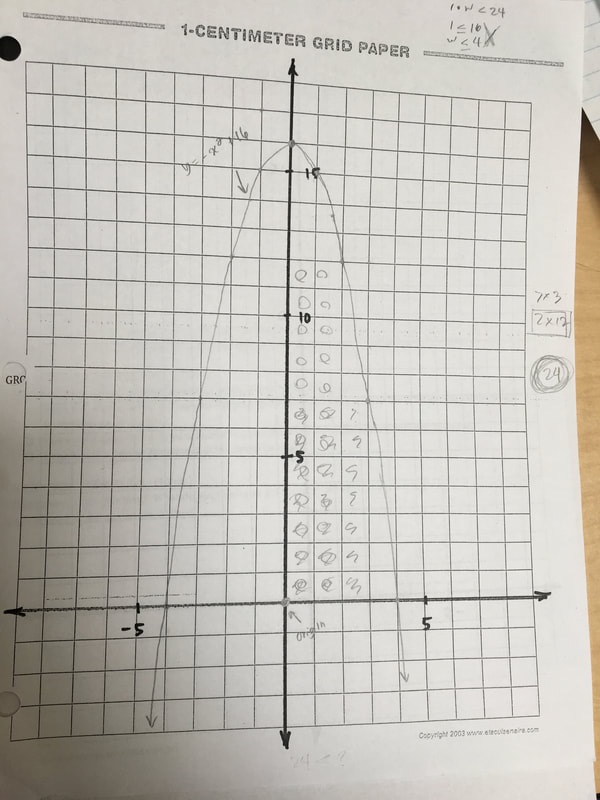
For the final diagram (shown below), I plotted a point at the origin again. This time I drew out a parabola, using the function y = 16 - x^2. Like my initial attempt, my last two points met up the point on the line to the positive x and y axis. |
|
Initially when I was trying to solve for the maximum area, I went through all of the integers on the x-axis from 1-4, where the parabola ended. I found that the highest areas were 24 and 21. I got these areas from using 2 and 3 as the width of the rectangle or x-value on the graph. When I chose 2 as a value of x, I followed it up on the y-axis of the parabola to see the highest value of y I could get. The highest y-value ended up being 12. This means 12 was our height. I multiplied 2 and 12 and that is how I got the area of 24. I did the same for the x-value of 3 after to see which gave me a bigger area. |
Our final generalized for the maximum area of the rectangle ended up being A = -x^3 + 16x. We found this because we knew that the area of a rectangle is equal to the length multiplied by the width. Our length and width in this problem is essentially x and y, which means A = xy. We know that our width is a point on the x-axis. In the original problem statement they give us the function, y = 16 - x^2. If we substitute the y in the equation A = xy, using the function y = 16 - x^2 we get A = -x^3 + 16x.
Our final generalized function for maximum perimeter of the rectangle was P = -2x^2 +2x +32. We found this because we know that the perimeter of a rectangle is all the sides added together. If our sides were x and y, we knew the equation we were working with was P = 2(x + y). Like we did for the maximum area, if we substitute the y in the equation P = 2(x + y), using the function y = 16 - x^2 we get P = -2x^2 +2x +32.
We knew both of these function were correct because, when we graphed them, their vertex gave us the maximum area and maximum perimeter.
Our final generalized function for maximum perimeter of the rectangle was P = -2x^2 +2x +32. We found this because we know that the perimeter of a rectangle is all the sides added together. If our sides were x and y, we knew the equation we were working with was P = 2(x + y). Like we did for the maximum area, if we substitute the y in the equation P = 2(x + y), using the function y = 16 - x^2 we get P = -2x^2 +2x +32.
We knew both of these function were correct because, when we graphed them, their vertex gave us the maximum area and maximum perimeter.
Solution
The solution for the maximum perimeter is equal to 32.5 with the side lengths (0.5, 15.75). We found this by completing the square and turning the perimeter formula we constructed into vertex form. Once we found the vertex, we knew that the x-value was equal to the width and the y-value was equal to the maximum perimeter.
The solution for the maximum area is equal to 24.633609. Our groups initial guess for the maximum area was somewhere in between 21 and 24. Our final area, to the nearest hundredth ended up being 24.633609 with the side lengths (2.31, 10.6639). For the area we started off with just integers and looked at the biggest areas. From there we took the x-values and got into decimals. We did this until the hundredths place and that's how we found 24.633609.
The solution for the maximum area is equal to 24.633609. Our groups initial guess for the maximum area was somewhere in between 21 and 24. Our final area, to the nearest hundredth ended up being 24.633609 with the side lengths (2.31, 10.6639). For the area we started off with just integers and looked at the biggest areas. From there we took the x-values and got into decimals. We did this until the hundredths place and that's how we found 24.633609.
Group Test / Individual Test
Our group prepared for the group quiz by going over the original problem and going step by step through the new version of the problem, making sure that we understood every aspect. I think during the group quiz my group worked together very well. We communicated, and made sure we were all on the same page. On the individual quiz, I was confident in the first two problems asking to find the area and perimeter of a rectangle with a given width. I struggled a lot with the honors question. I was going back and forth to try to get the x on one side. The overall experience of the group quiz was a little stressful because we were faced with the same kind of problem but we were working in two quadrants. We had to make sure we were changing something from what we previously worked on in class. After a little while, my group was able to figure it out and find the answers.
Evaluation / Reflection
Something that pushed my thinking was during the group test. It took me awhile to realize how I had to change the equation for the maximum area and perimeter in order to accommodate for two quadrants instead of one. I think the thing I got the most out of it was exercising my ability to solve a problem multiple ways. For the maximum perimeter I was able to plug and chug, and I also learned how to solve it using vertex form. If I were to grade myself on this unit I would give myself an A because I think I was able to help my group mates understand the math topics we were working with and communicate well during group work time.
Cow Problem Write Up
Problem Statement
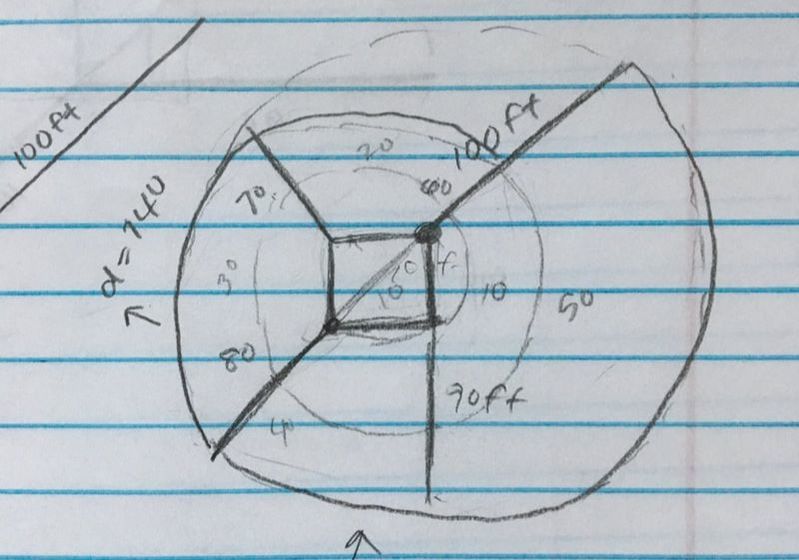
There is a 10' by 10' barn. A cow is attached to a corner of the barn with a 100' rope. We need to figure out what area of land the cow can graze.
Process
|
My final, accurate diagram maximized the cow's rope to give it a bigger area to graze. Instead of wrapping around the barn to get to the other side, once the cow went one way and reached a certain point it would turn around and meet the other point on the other side. The little dimple is the point that I am talking about. |
Once we got our final diagram, we needed to break up the diagram into manageable pieces in order to find the area of it. When we have this weird shape, there is no formula to find the area of it. But if we can break up our weird shape into shapes we know and have formulas that we know can get us the area, finding the area of the whole thing is easier.
The dimensions we needed in order to solve the problem were:
- the diagonal length inside the barn
- the height of the triangle in between the two sectors
Solution
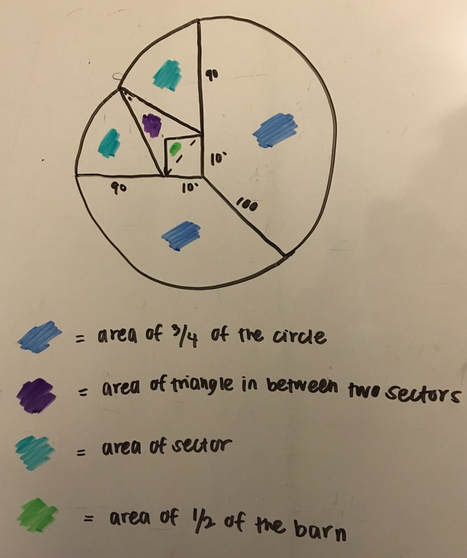
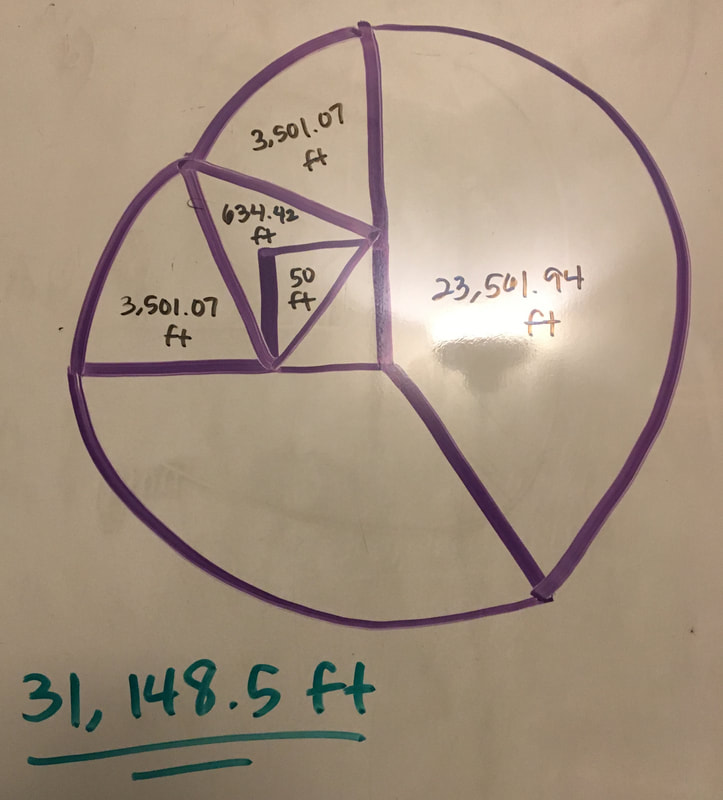
The solution to find the total area of the Cow Problem is: (area of the 3/4 of the circle) + (area of triangle in between two sectors) + 2(area of sector) - (area of 1/2 of the barn) = total area the cow can graze
In order to explain how we solved this problem using the formula above, we need to break it up into different parts to use the multiple equations and formulas we learned.
1. Area of a circle = πr^2
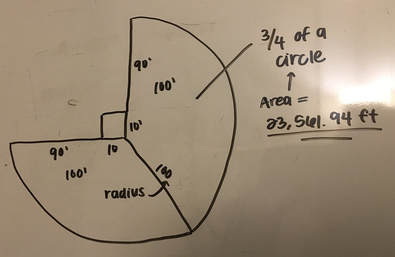
For the 3/4 of a circle, we used the formula for the area of a circle, which is A=πr^2, and multiplied it by 3/4.
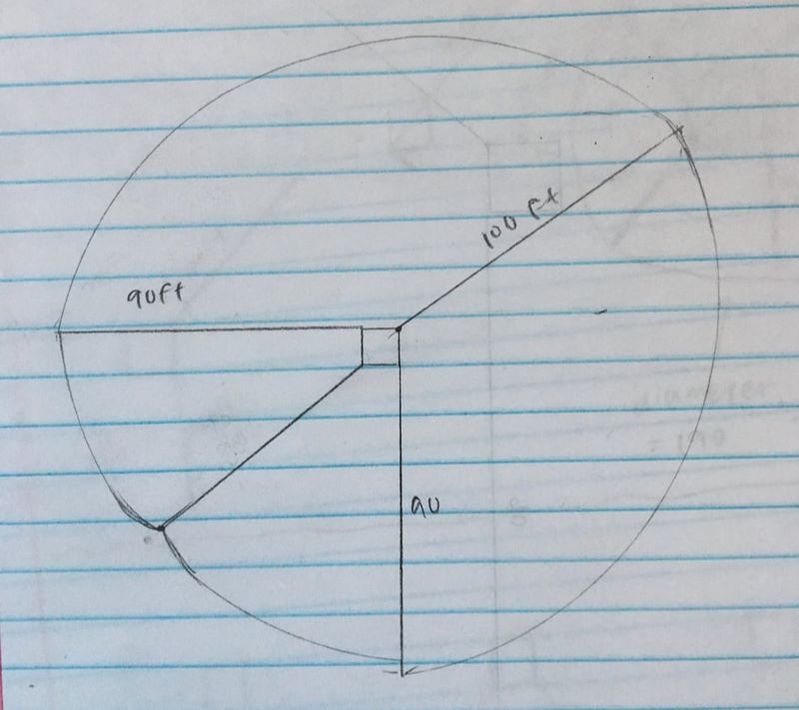
The radius was 100 because that's how long the rope was. When we plugged it into the formula we got 10,000π. 10,000π was the area of a whole circle but the cow could only graze 3/4 of a circle with the radius 100. That is why we multiplied it by 3/4. This got us with the area of 23,561.94 ft.
1. Area of a circle = πr^2
For the 3/4 of a circle, we used the formula for the area of a circle, which is A=πr^2, and multiplied it by 3/4.
The radius was 100 because that's how long the rope was. When we plugged it into the formula we got 10,000π. 10,000π was the area of a whole circle but the cow could only graze 3/4 of a circle with the radius 100. That is why we multiplied it by 3/4. This got us with the area of 23,561.94 ft.
|
2. The Pythagorean Theorem: a^2 + b^2 = c^2
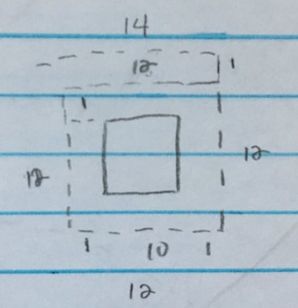
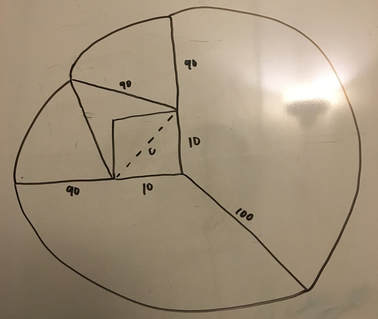
In order to find the area of the triangle indicated below, we first need to figure out the diagonal length going across the barn. We can find this using the Pythagorean theorem. The diagonal length is c in the equation because it is opposite the right angle in the triangle, making it the hypotenuse. We know that a is equal to 10 and b is equal to 10. We learned about radicals to help us with this step. When we solve the equation out we get c=10√2. |
|
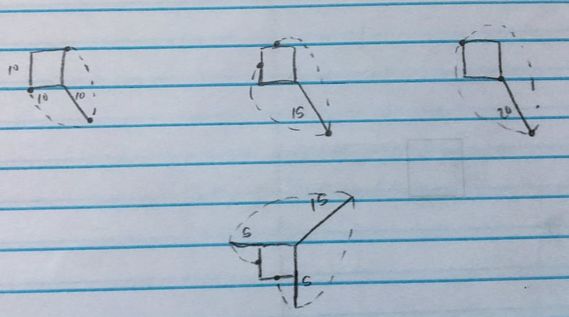
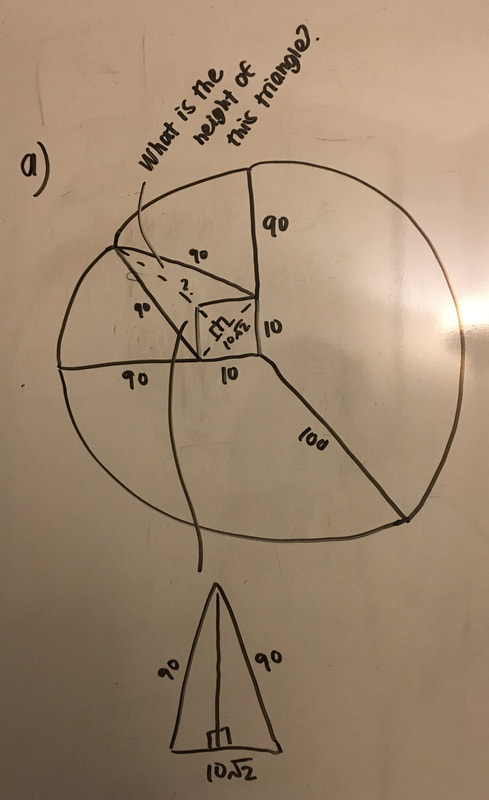
a) Now that we have the base of the triangle's length, we need to find the height. If we split the triangle straight down the middle from it's highest point to the base we get two symmetrical right triangles. Now that we have a right angle we can use the Pythagorean Theorem again!
b) If we are looking at just the left right triangle, we know that the hypotenuse in this triangle is 90 ft. because from the bottom left corner of the barn anywhere the rope goes is equal to 90 ft. Once the cow goes past the upper left corner of the barn the rope becomes 80 ft. c) We know the base of the right triangle is 5√2 because the whole base was equal to 10√2. When we spilt the triangle in half, we split the base in half making it 5√2. d) We have two lengths in the equation so we can solve for the third one. This time we have to be careful with what numbers we have and what number we're trying to solve for. We have the hypotenuse and the base. That means we have c and b of the equation. When we solve it out, we get the height of the triangle equals 89.72 ft. |
|
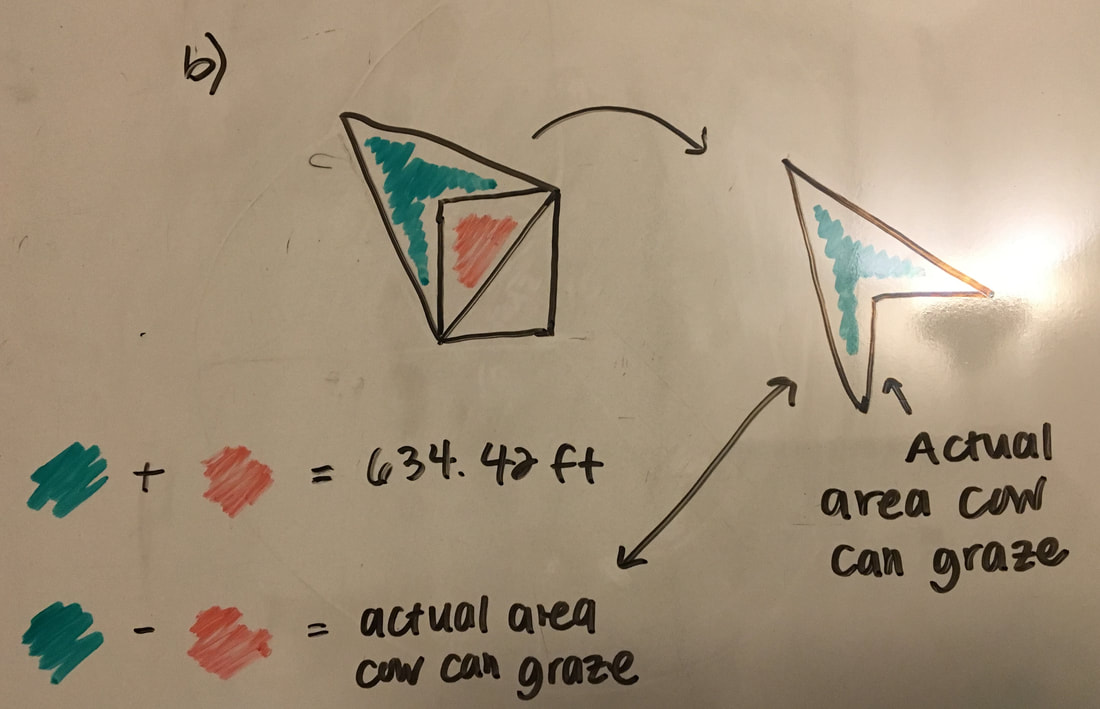
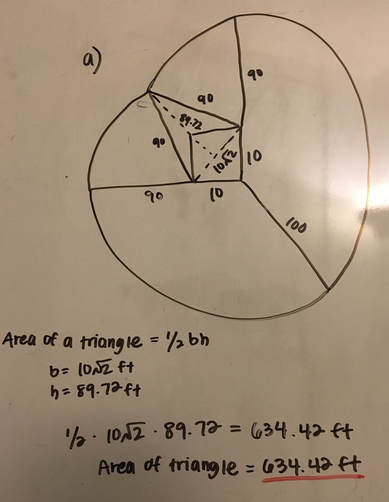
3. Area of a triangle = 1/2bh
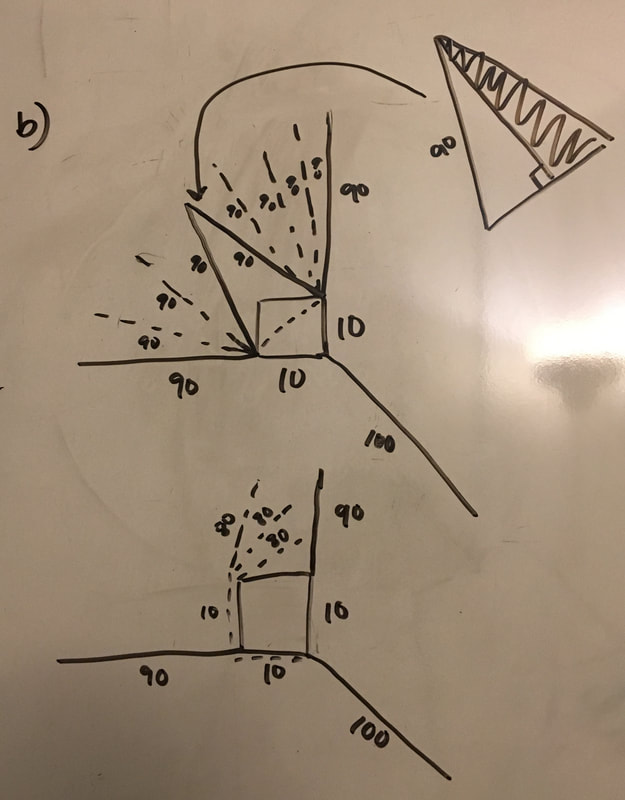
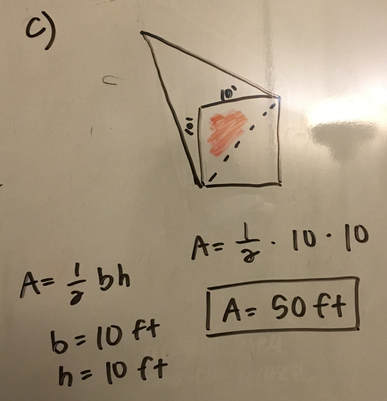
a) Now we have all the numbers we can find the area of the triangle. The height is 89.72 and the base is 10√2. When we solve it out we get the area of the triangle equals 634.42 ft. b) There is one more catch to this. We have been solving for this triangle but a part of the triangle is in the barn. The cow is attached to the outside of the barn and the barn has no doors. The actual shape we are trying to calculate looks like the one in the picture shown to the right. This means we have to subtract the part of the barn that we have been including in our calculations to find the real area of the weird shape. c) We have been including exactly half of the barn in our calculations which is the shape of a triangle. We can use the formula for the area of a triangle again to find the area we need to subtract. The height of the barn is 10 and the base of the barn is 10. After we plug it into the formula we get the area of the triangle equals 50 ft. |
4. Inverse Trigonometry
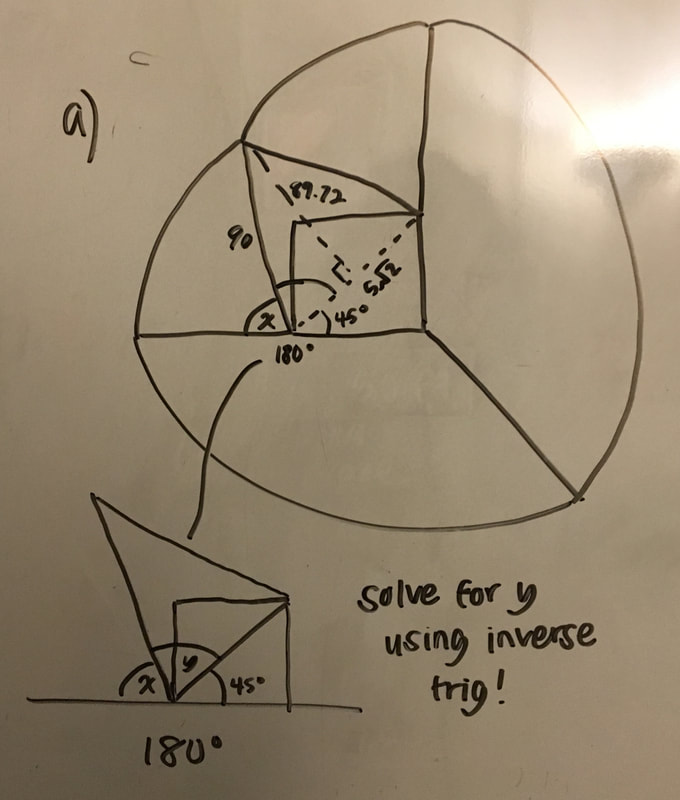
All we have left to do is find the area of the sectors. Inverse trigonometry is very important in helping us find the area of them.
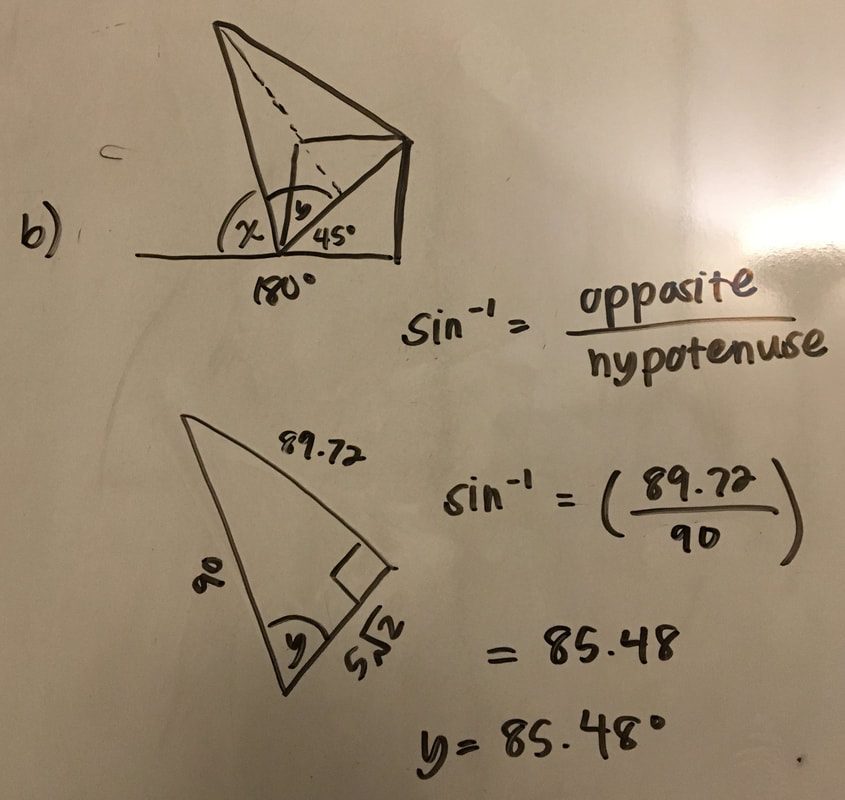
a) Our goal is to find the angle x in the diagram below. In order to do this we need to use the information we already know. We know that a straight line is equal to 180°. We know the very left angle is 45° because it's exactly half of the square barn which is a right angle. We can solve for the middle angle using inverse trig!
b) Because we have all three side lengths of the triangle we can use any function (sine, cosine, or tangent) to find the angle (y). Let's use sine. Sine is opposite divided by hypotenuse. The opposite of angle y is 89.72 and the hypotenuse is 90. After plugging it into the calculator, you get angle y is equal to 85.47.
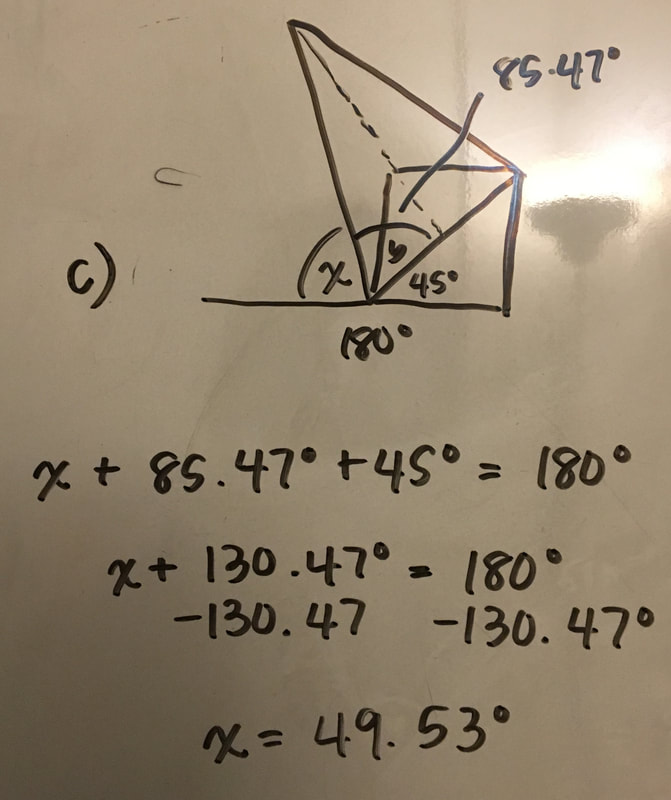
c) We have three things that equal 180°. We have figured out two of those values so now we can solve for the third. Angle x + angle y + 45° = 180°
After solving this equation we got the angle of the sector was equal to 49.53°.
All we have left to do is find the area of the sectors. Inverse trigonometry is very important in helping us find the area of them.
a) Our goal is to find the angle x in the diagram below. In order to do this we need to use the information we already know. We know that a straight line is equal to 180°. We know the very left angle is 45° because it's exactly half of the square barn which is a right angle. We can solve for the middle angle using inverse trig!
b) Because we have all three side lengths of the triangle we can use any function (sine, cosine, or tangent) to find the angle (y). Let's use sine. Sine is opposite divided by hypotenuse. The opposite of angle y is 89.72 and the hypotenuse is 90. After plugging it into the calculator, you get angle y is equal to 85.47.
c) We have three things that equal 180°. We have figured out two of those values so now we can solve for the third. Angle x + angle y + 45° = 180°
After solving this equation we got the angle of the sector was equal to 49.53°.
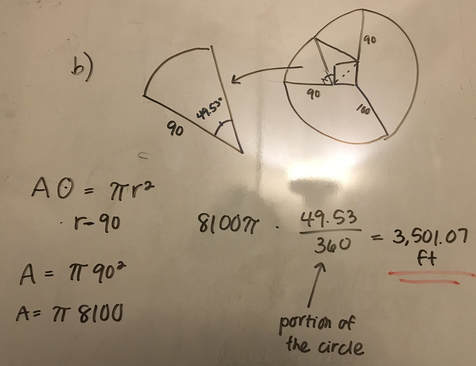
5. Area of a sector = πr^2 x degree of sector/360
a) The second to last step is to solve for the area of the sector. A sector is essentially a part of a circle. The degree of straight line is 180° and the degree of a right angle is 90°. If we think about a quarter or a half of a circle, those angles are 90 and 180° respectively. If a quarter of a circle is equal to 90°, that makes sense because a full circle is 360°. 90/360 equals a quarter. The same goes for half of a circle. 180/360 equals one half. This means that whatever degree a sector is, if we put it over 360 that gets us the portion of the circle. If we multiply the area of a circle times the portion that we want (the sector), we get the area of just the sector.
b) We know the angle of our sector is 49.53° and the radius of our circle is 90 ft. We can plug in these numbers to our equation and we get the area of the sector equals 3,501.07 ft.
a) The second to last step is to solve for the area of the sector. A sector is essentially a part of a circle. The degree of straight line is 180° and the degree of a right angle is 90°. If we think about a quarter or a half of a circle, those angles are 90 and 180° respectively. If a quarter of a circle is equal to 90°, that makes sense because a full circle is 360°. 90/360 equals a quarter. The same goes for half of a circle. 180/360 equals one half. This means that whatever degree a sector is, if we put it over 360 that gets us the portion of the circle. If we multiply the area of a circle times the portion that we want (the sector), we get the area of just the sector.
b) We know the angle of our sector is 49.53° and the radius of our circle is 90 ft. We can plug in these numbers to our equation and we get the area of the sector equals 3,501.07 ft.
|
6. Add everything together!
Going back to the formula we wrote before, (area of the 3/4 of the circle) + (area of triangle in between two sectors) + 2(area of sector) - (area of 1/2 of the barn) = total area the cow can graze, now we have all the values we need to solve it out! Area of the 3/4 of the circle = 23,561.94 ft. Area of triangle in between two sectors = 634.42 ft. Area of sector = 3,501.07 ft. Area of 1/2 of the barn = 50 ft. 23,561.94 + 634.42 + 2(3,501.07) - 50 = 31,148.5 ft. The cow can graze an area of 31,148.5 ft. |
Evaluation / Reflection
This thing that pushed my thinking the most was definitely just initially drawing the shape we had to work with. I had my head stuck on the cow just wrapping itself around the barn over and over again. It took me awhile to finally understand how to maximize its space and why that shape looked the way it did. I think the thing I got the most out of it was to be careful about not overlooking and overthinking things. Be open to things that aren't the first thing that pops into your head when you read a problem. Other things work too. Also, I made many mistakes purely based on just going to fast. Sometimes its good to go slow to so you know what you're doing. I think the group quiz affected my learning in a positive way. I've always said that understanding how to do something is one thing and being able to teach it to someone is a whole other thing. You know you fully understand something when you can teach it and I think that's what helped me fully understand the cow problem.
If I were to grade myself on this unit, I would give myself an A because I stayed invested and I communicated with my group. I made sure I understood the concepts I was being taught by the practice packets. If I found that I wasn't getting the answer, and I didn't know why I would ask Mr. Carter why that was. I didn't stop until I understood. I also felt that I was able to help my group my members. I would constantly ask them if what I was doing made sense and if it didn't, I would find another way to explain it.
If I were to grade myself on this unit, I would give myself an A because I stayed invested and I communicated with my group. I made sure I understood the concepts I was being taught by the practice packets. If I found that I wasn't getting the answer, and I didn't know why I would ask Mr. Carter why that was. I didn't stop until I understood. I also felt that I was able to help my group my members. I would constantly ask them if what I was doing made sense and if it didn't, I would find another way to explain it.