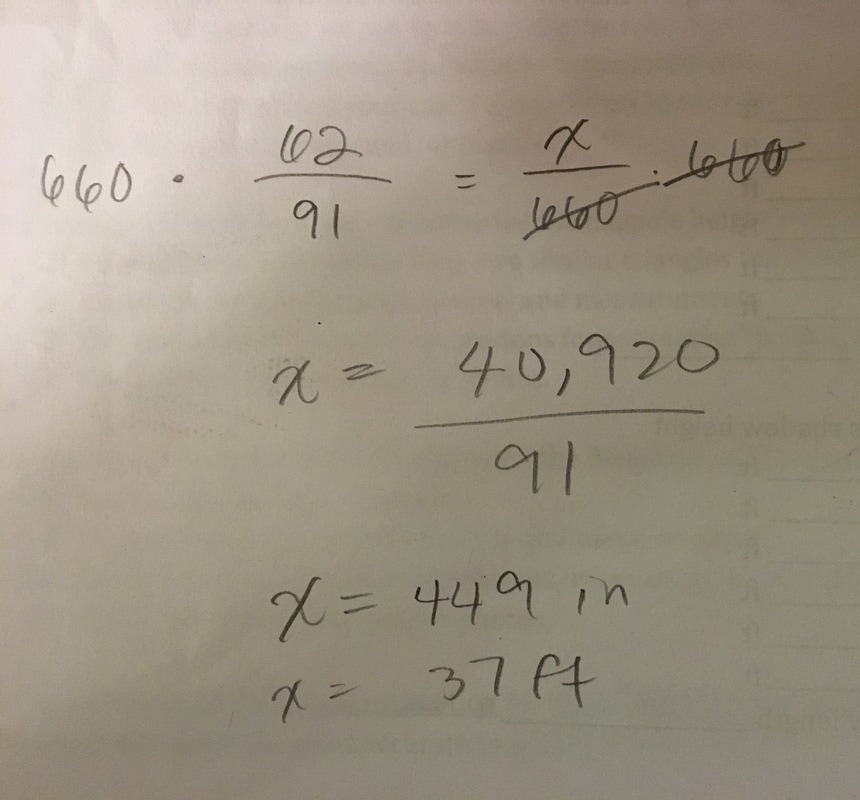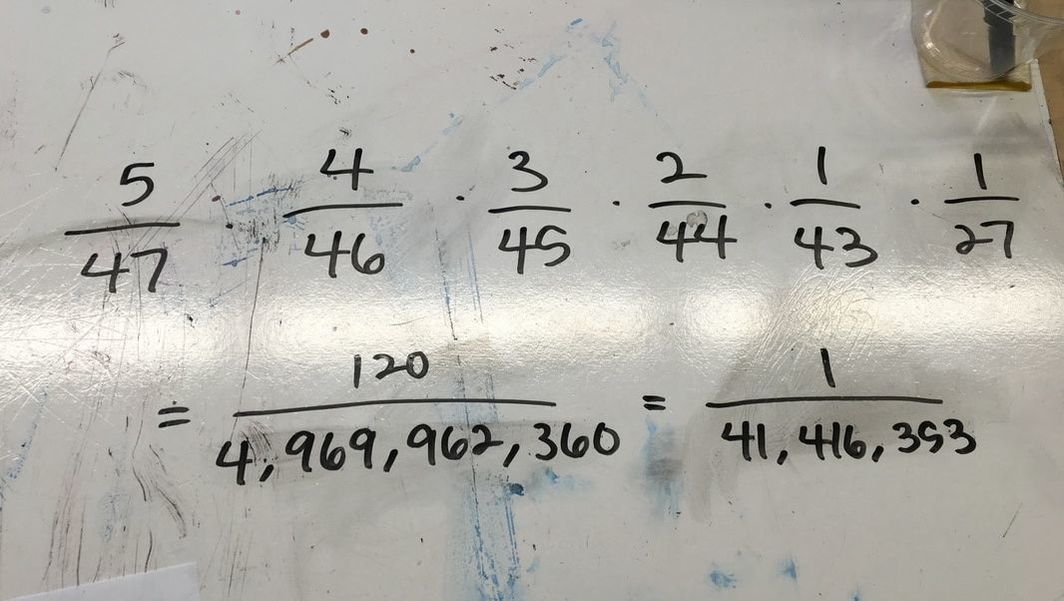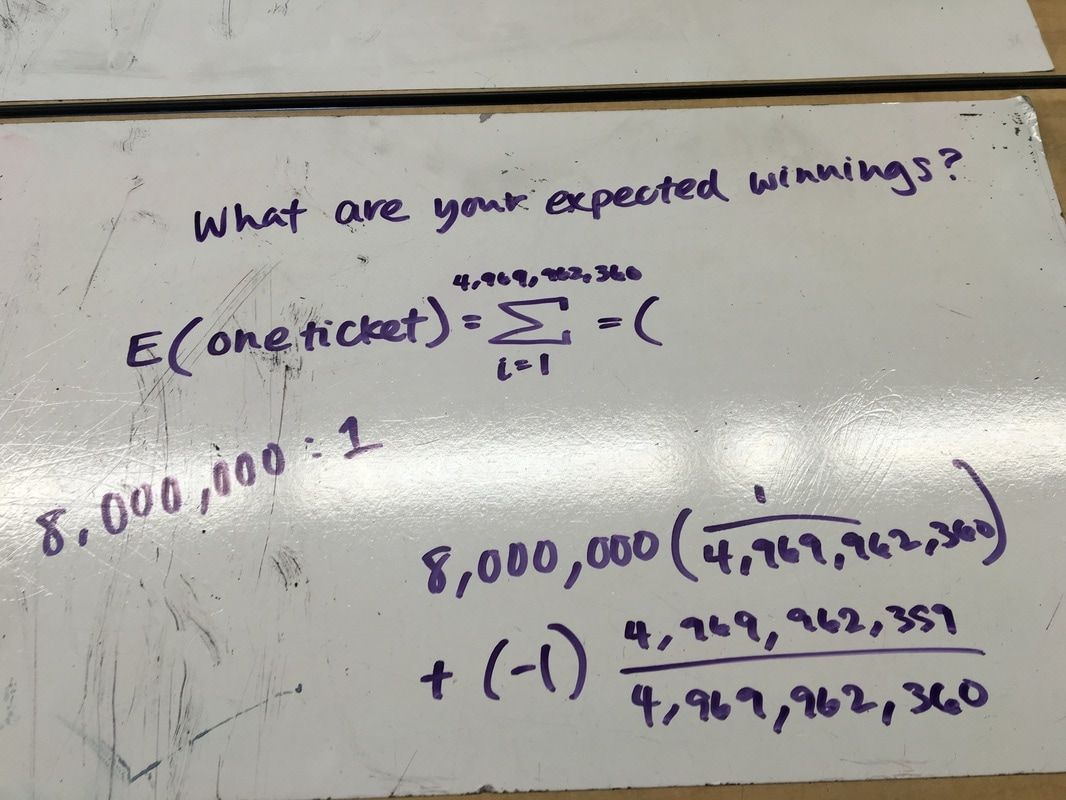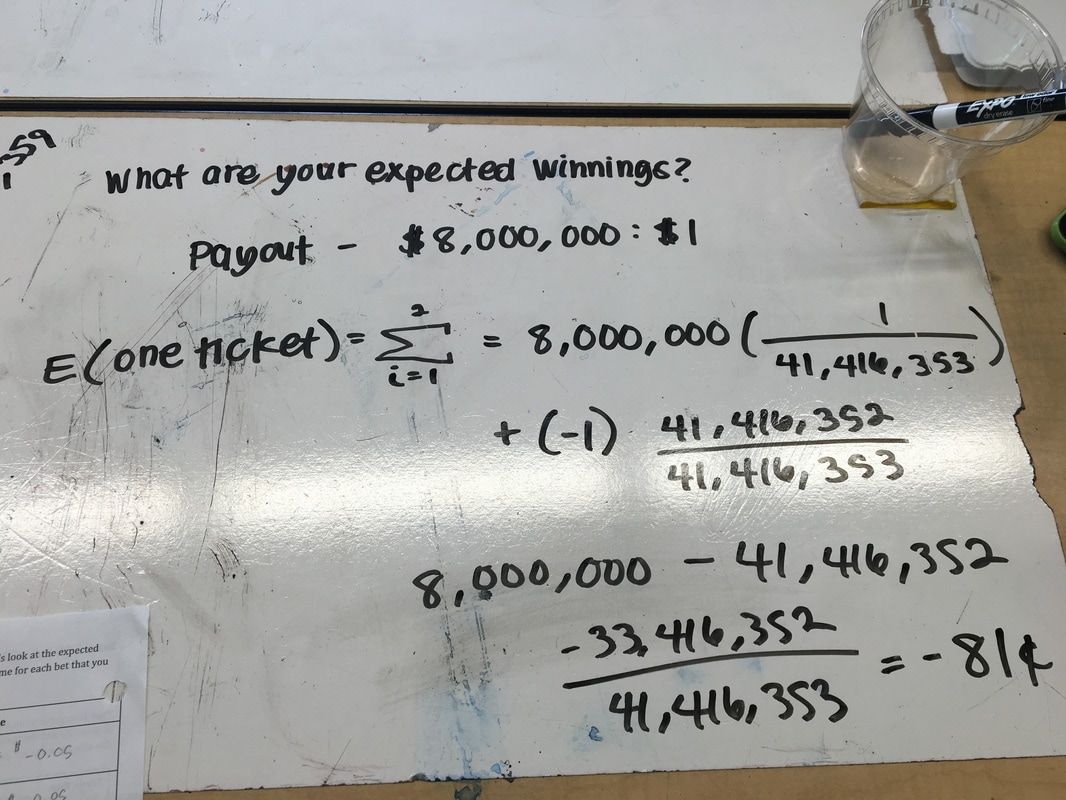Height of the Flagpole Write Up
My initial guess for the height of the flagpole before we took any measurements was 68.75 ft
My estimation using the shadow method was 37 ft
My estimation using the mirror method was 23 ft
My estimation using the isosceles method was 24 ft
My estimation using the shadow method was 37 ft
My estimation using the mirror method was 23 ft
My estimation using the isosceles method was 24 ft
Problem Statement
High Tech wants to buy a bigger flag but the biggest size you can get depends on how tall the flagpole is. We can't find the height of the flagpole just by measuring it but there is other ways using similarity. What is the height of the flagpole?
Process & Solution
For the launch of this problem, we first made an initial guess. My guess was between 50-90 ft. We went outside to take a look at the flagpole. Afterwards, we made a more refined guess. The minimum height I thought the flagpole would be was 30 ft and the maximum height I thought the flagpole would be was 80 ft.
Similarity roots from the word 'same' or 'similar'. Two objects are similar if they have the same shape. With similar shapes, lengths may vary but angles must be the same. In order for two shapes to be similar they're corresponding side ratios have to be equal.
Similarity roots from the word 'same' or 'similar'. Two objects are similar if they have the same shape. With similar shapes, lengths may vary but angles must be the same. In order for two shapes to be similar they're corresponding side ratios have to be equal.
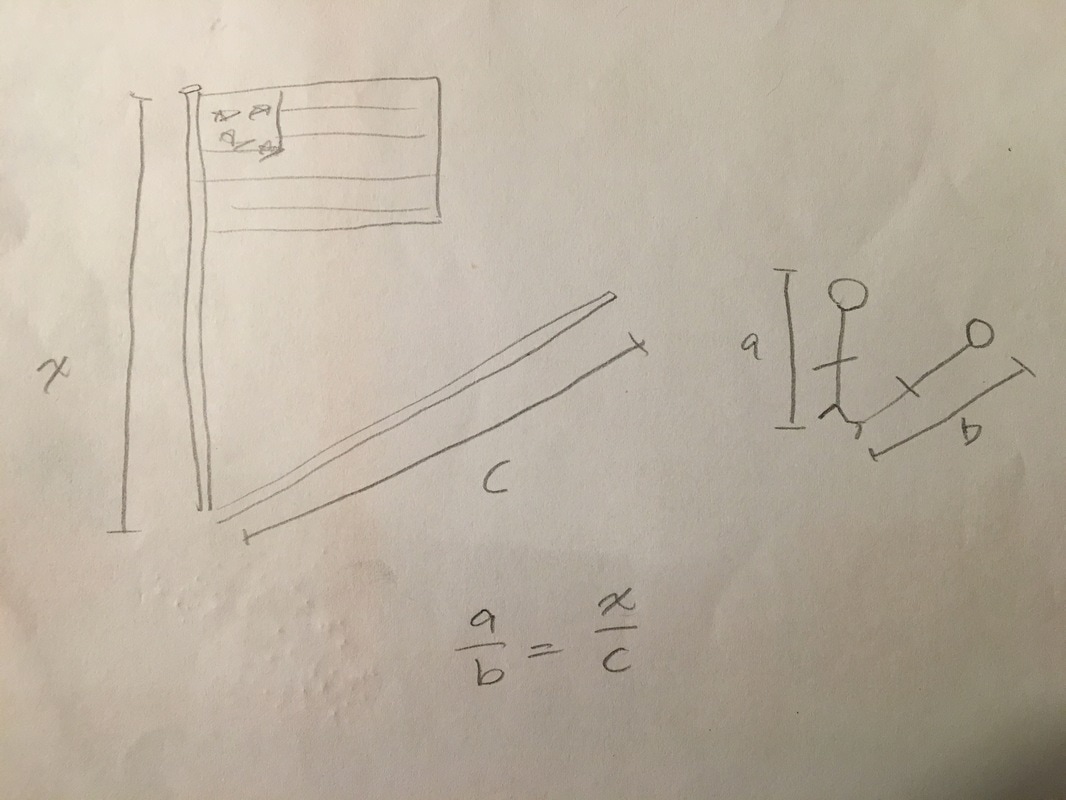
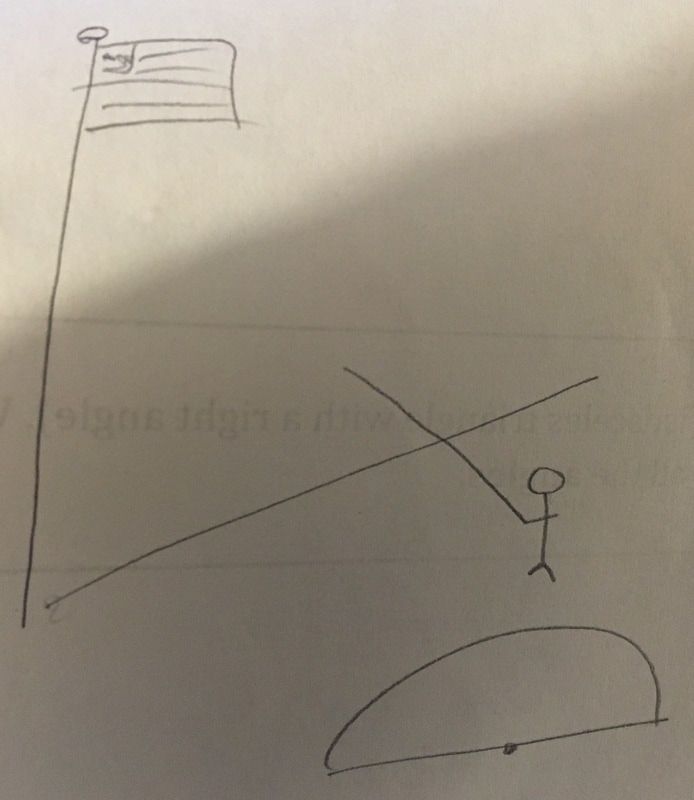
Shadow Method
If we don't know the height of the flagpole but we can measure its shadow we can use someone's height and the length of their shadow to set up an algebraic equation, like the example shown on the left.
We went outside and measured the shadow of the flagpole and our own shadow. The flagpole's shadow was 660 inches and my group's average shadow length was 91 inches.
My group's average height was 62 inches. We plugged in the numbers like in the picture above and created the equation below. We ended up the flagpole's height being 37 feet.
This method uses the theorem angle, angle.
We went outside and measured the shadow of the flagpole and our own shadow. The flagpole's shadow was 660 inches and my group's average shadow length was 91 inches.
My group's average height was 62 inches. We plugged in the numbers like in the picture above and created the equation below. We ended up the flagpole's height being 37 feet.
This method uses the theorem angle, angle.
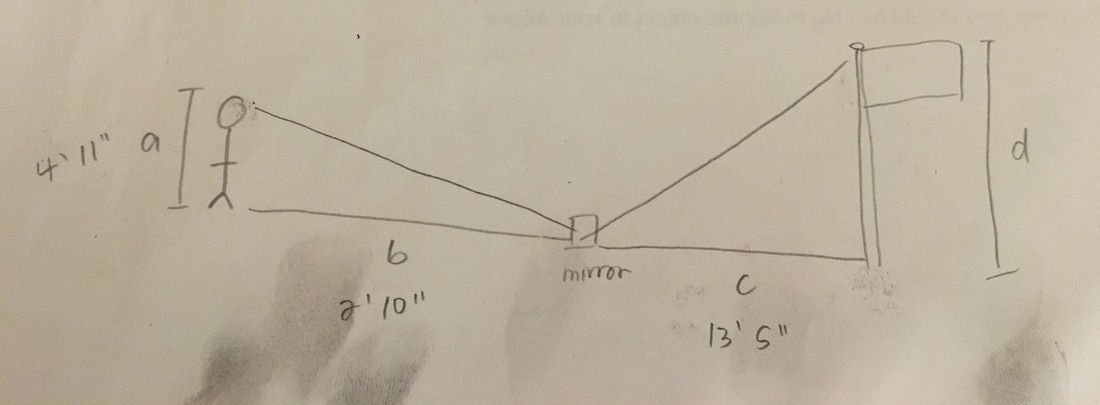
Mirror Method
We can form two similar triangles using the mirror method because we have two right angles at the stick figure's feet and at the bottom of the flagpole. We know opposite angles are equal when we have intersecting lines so we know the two angles that meet at the mirror are equal as well. Two of the same angles are enough to prove two triangles are similar.
There are four inputs in this method:
We placed a mirror on the floor and had someone move until they could see the object we wanted to measure in the mirror. We measured the distance from the person to the mirror and the distance from the mirror to the point directly below the object. We knew the person's height and all we needed to do was figure out our object's height.
The four inputs for the height of the flagpole are:
There are four inputs in this method:
- The person's height - a
- The horizontal distance from person to mirror - b
- The horizontal distance from mirror to object - c
- The object's height - d
We placed a mirror on the floor and had someone move until they could see the object we wanted to measure in the mirror. We measured the distance from the person to the mirror and the distance from the mirror to the point directly below the object. We knew the person's height and all we needed to do was figure out our object's height.
The four inputs for the height of the flagpole are:
- Luz's height - 4'11" or 59"
- The horizontal distance from Luz to the mirror - 2'10" or 34"
- The horizontal distance from the mirror to the flagpole - 13'5" or 161"
- The flagpole's height - d
Using this information we can set up our equation multiple ways to solve for the height of the flagpole. When setting up the equation, we have to be sure that we are lining up corresponding sides or else the equation is incorrect. We changed all the inputs into inches to make the math easier. Below are two ways you can solve for d:
The first way is comparing the ratios person's height to distance from mirror and height of flagpole to distance from mirror. The second way compares the ratios the person's height to the flagpole's height and the distance from the person to the mirror to the distance from the flagpole to the mirror. Both get you the same answer, which equals to 23 feet.
This method uses the theorem angle, angle.
This method uses the theorem angle, angle.
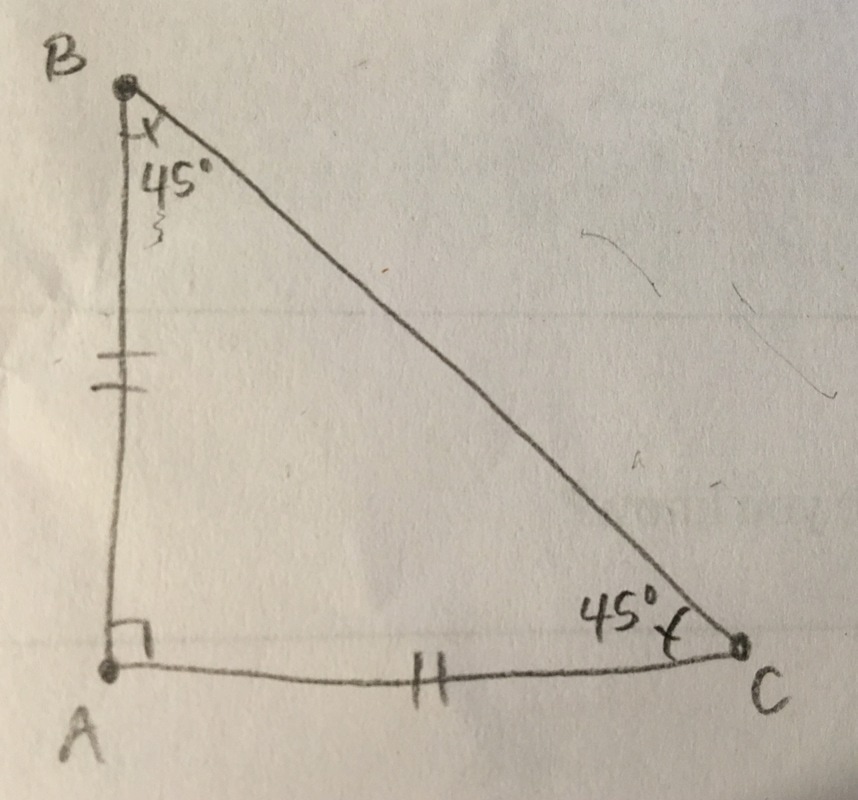
Isosceles Method
An isosceles triangle is a triangle with two equal lengths and two equal angles. We used the rules of an isosceles triangle as another way to figure out the height of the flagpole.
For this method we had someone stand at a point on the shadow of the flagpole. They pointed to the very top of the flagpole which created a triangle, one point being the person's feet, one point being the top of the flagpole and one point being at the bottom of the flagpole. Another person was a couple feet away with a protractor. They told the person pointing to the flagpole to move along the shadow of the flagpole until their arm was pointed at 45 degrees. We know that the bottom of the flagpole is 90 degrees. If we made the angle at the person's arm 45 degrees we know that the angle at the top of the flagpole is 45 degrees because of the 180 degrees triangle rule. Because there are two of the same angle we know the triangle we are making is an isosceles triangle. That means that the distance the person was standing away from the bottom of the flagpole is the height of the flagpole.
We ended up getting 24 feet using this method.
For this method we had someone stand at a point on the shadow of the flagpole. They pointed to the very top of the flagpole which created a triangle, one point being the person's feet, one point being the top of the flagpole and one point being at the bottom of the flagpole. Another person was a couple feet away with a protractor. They told the person pointing to the flagpole to move along the shadow of the flagpole until their arm was pointed at 45 degrees. We know that the bottom of the flagpole is 90 degrees. If we made the angle at the person's arm 45 degrees we know that the angle at the top of the flagpole is 45 degrees because of the 180 degrees triangle rule. Because there are two of the same angle we know the triangle we are making is an isosceles triangle. That means that the distance the person was standing away from the bottom of the flagpole is the height of the flagpole.
We ended up getting 24 feet using this method.
My best final estimation for the height of the flagpole is 23 feet because I think the mirror method is the most accurate. Our shadow method estimation was way off from the other two and when we were dong the isosceles method we didn't get 45 degrees right on the dot.
Problem Evaluation
This problem was interesting to me, I enjoyed how there were many ways to solve it The isosceles method pushed my thinking because I had to think outside of the box and connect the pieces about the rules of isosceles triangles in order for me to understand. I think the most I got out of this problem was discovering those different ways to solve it. A lot of the times I stick to my comfort zone and never stray away from it but this problem taught me new methods.
Self Evaluation
If I were to grade myself on this similarity unit I would give myself a B. I admit, sometimes I would get off task but for the most part I was able to work with my group members, especially Luz to solve the problems. We would also help Paola and Rebecca and we made sure that we understood each method.
Edits
Rebecca told me to add the theorems for each of the methods.
California Super Lotto Write Up
Problem Statement
In the beginning of this unit we made a wild guess on the chances of us winning the California Super Lotto. Throughout the unit we learned the skills we needed in order to solve this problem. There are three parts to the problem:
The rules to the the CA Super Lotto are pretty simple:
- How many different number combinations are possible for a CA Super Lotto ticket?
- What is the probability of winning the CA Super Lotto ticket?
- If you match all 6 numbers, you win $8,000,000. It costs $1 to play. What are your expected winnings?
The rules to the the CA Super Lotto are pretty simple:
- Choose any 5 numbers between 1-47 (these numbers do not repeat)
- Pick a mega number between 1-27 (this number can repeat)
- Match all 5 numbers and the mega number and you win!
Process & Solution
|
On the first day of launching this problem we kicked it off by playing the lottery together. Mr. Anatole offered to give us $20 if we didn't risk it but even more extra credit if we took the chance and won the lottery.
My initial guess for the odds of winning the CA Super Lotto was 1 out of every 15 million people. But I decided not to risk it and get my free extra credit points. Turns out, I made the right decision because everyone who did decide to risk it didn't win. |
How many different number combinations are possible for a CA Super Lotto ticket?
I approached this problem by simplifying it. Instead of having five slots, there are two. And instead of having 47 numbers there are only 3. After writing out all the possibilities, I realized that you just need to multiply two numbers because there are two slots and the first number is 3 because there are 3 numbers to choose from and the second number is 2 because there are now 2 numbers to choose from since you took one out already.
Using this I expanded the problem back to it's original numbers and made five slots and one more for the mega number. I put 27 for the mega number because that is all the different possibilities. And for the five slots I put 47 for the first one and then 46 for the second one because we already took one out. I did this until all five slots were filled and multiplied all six numbers to get a total of 4,969,962,360 combinations.
Using this I expanded the problem back to it's original numbers and made five slots and one more for the mega number. I put 27 for the mega number because that is all the different possibilities. And for the five slots I put 47 for the first one and then 46 for the second one because we already took one out. I did this until all five slots were filled and multiplied all six numbers to get a total of 4,969,962,360 combinations.
What is the probability of winning the CA Super Lotto?
At first I thought the probability of winning was just 1 out of all the possible combinations, which is the picture on the left below. But then I learned that order doesn't matter in the lottery, meaning if the numbers 12345 were picked as the original five numbers I would still win if I wrote down 54321, or any combination of those numbers.
To find the total number of ways you can rearrange five numbers you just solve for 5!. It's finding the total amount of combinations with five numbers and five slots. 5! = 120. After I got 120, I put it over the total number of combinations and simplified it to get the probability of winning the CA Super Lotto to 1 out of every 41,416,353 people. My original guess was a few million off but that's okay!
To find the total number of ways you can rearrange five numbers you just solve for 5!. It's finding the total amount of combinations with five numbers and five slots. 5! = 120. After I got 120, I put it over the total number of combinations and simplified it to get the probability of winning the CA Super Lotto to 1 out of every 41,416,353 people. My original guess was a few million off but that's okay!
If you match all 6 numbers, you win $8,000,000. It costs $1 to play. What are your expected winnings?
At first I thought the probability of winning was 1 out of almost 5 trillion which was wrong but also I wrote down that the total possibilities was that number was also almost 5 trillion. That was wrong because you either lose or win in the lottery which means that number should have been 2.
The expected value of one ticket is -81 cents because I multiplied the money you earn if you win by the probability of winning and added it to the amount of money you lose if you lose by the probability of losing. This got me -81 cents, which means for every ticket someone buys, the CA Super Lotto makes 81 cents.
The expected value of one ticket is -81 cents because I multiplied the money you earn if you win by the probability of winning and added it to the amount of money you lose if you lose by the probability of losing. This got me -81 cents, which means for every ticket someone buys, the CA Super Lotto makes 81 cents.
Problem Evaluation
Finding the expected value and rethinking why we had to multiply the top part of the probability really pushed my thinking. I think finding the expected value was the thing I got the most out of this problem because it was a completely new concept to me and I was able to understand it by applying it to this problem.
Self Evaluation
If I were to grade myself on this probability unit I would give myself a B because I definitely wasn't on track the entire time. I would always make sure I was done with my work and I was asking questions if I get lost but once I was done, I was done. I didn't really help my group mates stay on task after I was done. However, throughout this week I have noticed a change in my behavior and I have been staying on task and helping out group members.
Edits
We did peer critique and I was not given any feedback for the write up.
Desmos Write Up
For the past two weeks we have immersed ourselves in the world of parabolas by using a program called Desmos. Everyday we learned a little bit more about transforming parabolas up, down, left, right, upside down, and skinnier or wider through five different activities. Desmos helped us gain a better understanding of quadratics and their graphs.
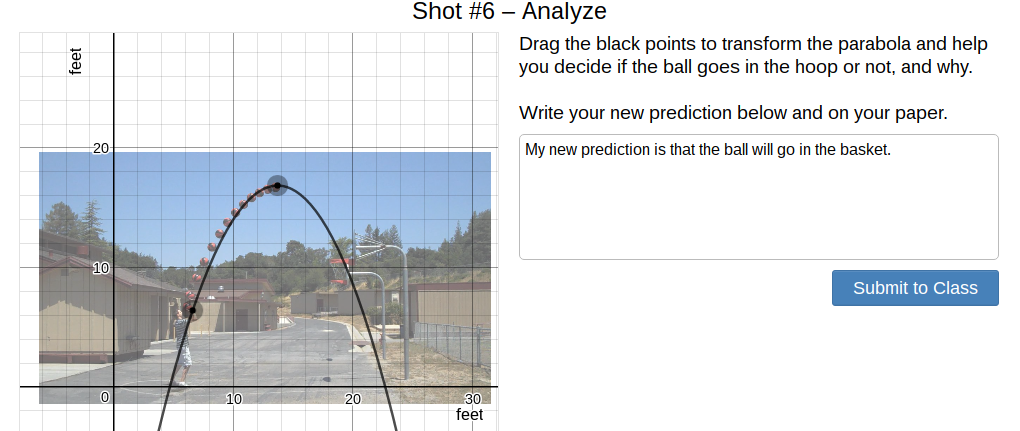
Basketball Problem
For the first day of working with parabolas we did the basketball problem. We had to predict if the guy in the picture was going to make the basket based on the parabola. I predicted that the ball would make it in the basket, from what the parabola showed me.
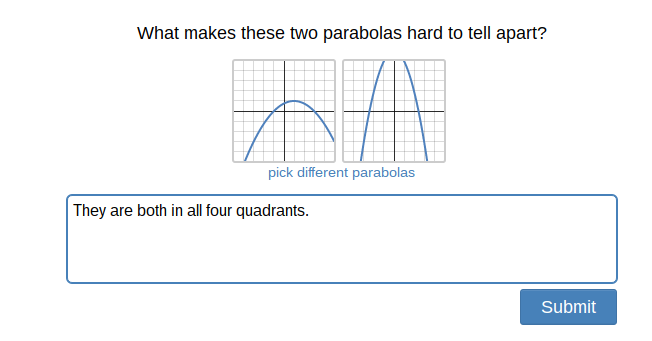
Polygraph 1
The second activity started off with us playing Guess Who but with parabolas. We were paired with a partner and had to guess which parabola they chose by asking them yes or no questions. If I had to guess between the two parabolas below I would ask, "Is the vertex of the parabola shown in the picture?"
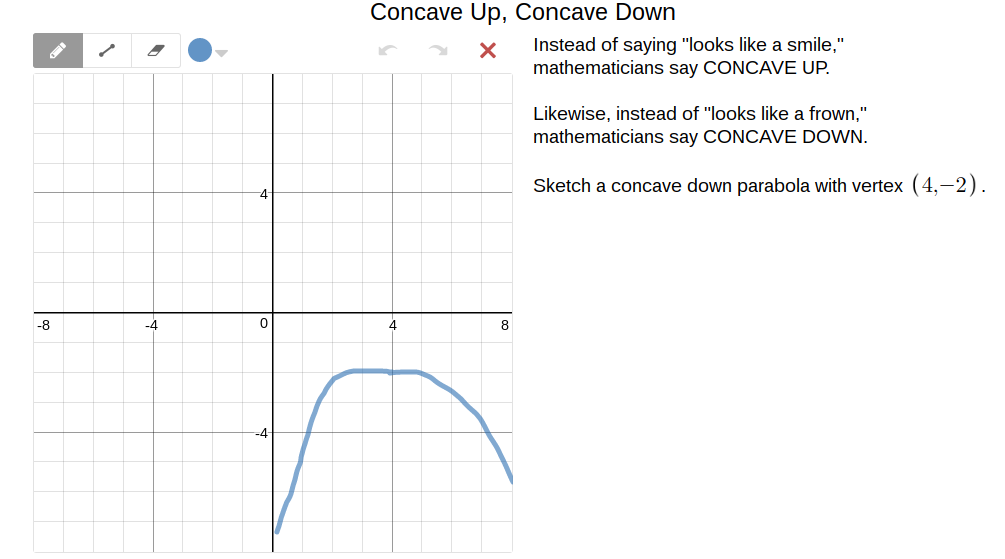
Polygraph 2
For the third activity we put names to the things we were doing. For the parabola below I used the knowledge I had learned of concave down and concave up to determine if the parabola was a frown or smile.
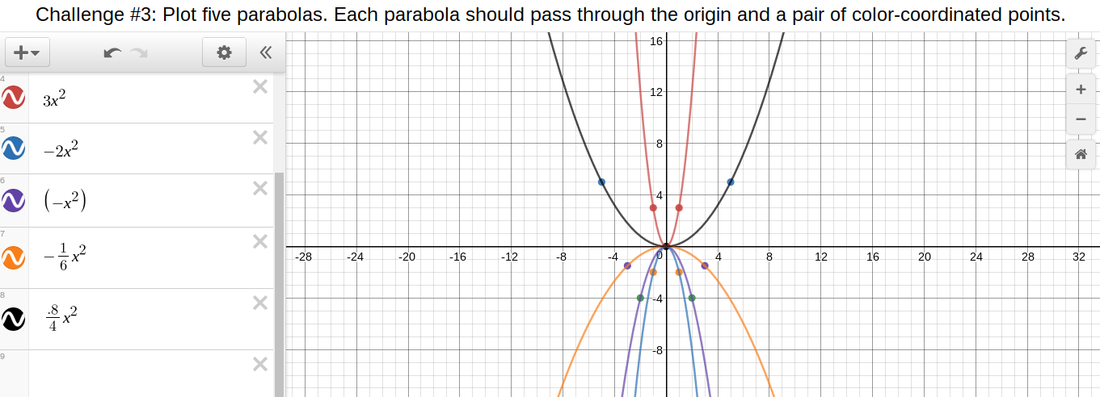
Match Problem
For the match problem, we were given specific points and we had to construct formulas to have the parabolas go through the points. The screenshot below shows the very specific fractions and decimals I had to put in order for the parabola to go through the points. It took a little playing around but I was able to get it.
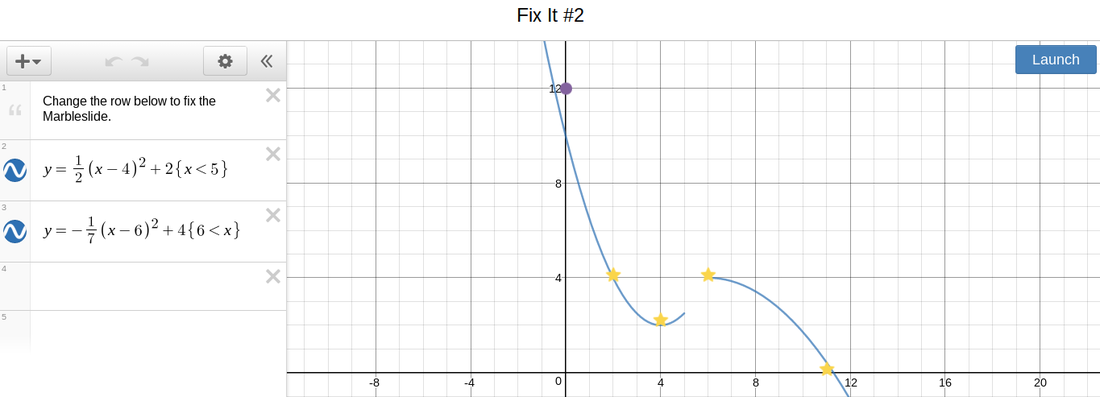
Marble Problem
For the last activity, we had to plot a parabola so that when a ball is released it will hit all of the stars. I played around with the domain so that the parabola would be broken up and I was able to collect all the stars.
7 Things I Learned about Parabolas using Desmos
- The turning point of the parabola is called a vertex.
- If the h is negative in the vertex form y=a(x-h)^2+K, then the vertex goes to the right on the x axis.
- If the h is positive in the vertex form y=a(x-h)^2+K, then the vertex goes to the left on the x axis.
- If the a is a fraction/decimal smaller than 1 in the vertex form y=a(x-h)^2+K, the parabola is wider.
- If the a is a number bigger than 1 in the vertex form y=a(x-h)^2+K, the parabola is slimmer.
- When a parabola looks like a smile it is called concave up.
- When a parabola looks like a frown it is called concave down.
Problem Evaluation
I thought Desmos made it really easy for us to follow and understand. The way they introduced parabolas to us with the basketball problem and then the Guess Who game was really fun and interactive because it's things we are familiar with and we were able o play with each other. Sometimes, I did feel like some of the activities were too repetitive but that wasn't too much of a problem.
Self-Assessment
Throughout the two weeks we worked on Desmos, I found at times I would get really lazy and not try anything, and other times I would be really invested in a problem. My goal for this semester was to be more aware of my group members and their progress. I really wanted to communicate and build a better understanding of everything through our conversations. I think I really slacked off on meeting this goal these past two weeks. When my group members did ask me for help, I helped them but that was the extent to our communication in regards to the parabolas.
Edits
Aija asked me, "Did this Desmos activity interest you?" This made me think about some of the times I got bored while using Desmos. I added a sentence on the problem evaluation portion about something I thought was not so great about Desmos.